Continuous simulation is something that can only really be accomplished with an analog computer. Using a digital computer one can approximate a continuous simulation by making the time step of the simulation sufficiently small so there are no transitions within the system between time steps. The premise for a continuous simulation is that there is a continuous time flow and the simulation is stepped in time increments.
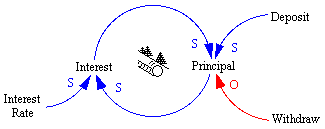
Suppose we consider the example of the interaction of the principle and interest associated with a savings account. This can be represented by a systems thinking diagram as follows:

This diagram indicates that Deposits increase the Principal and Withdraws decrease the Principal. Also, the Principal interacts with the Interest Rate, on some periodic basis, to create Interest. The Interest then serves to increase the Principal.
If we then turn this into a 10 year simulation with the assumptions that the Principal is initially $100, there are no Deposits or Withdraws, and an Interest Rate of 5% is paid once a year it might look like this in ithink.

With the following equations:
After a period of 10 years the Principal is about $155, and the graph looks rather continuous. This is because the simulation was stepped in increments of 1 year which is the same period over which the Interest is computed and applied to the Principal.

If we take the same simulation and run it in increments of 1 month, which means the Interest is calculated every 12 months the equation set becomes:
And the graph looks like:

Notice that the second graph indicates that the Principal after 10 years, or 120 months, is still about $155 yet the graph itself appears very discontinuous in nature.
The indication is that the operation of this simulation appears continuous or discrete depending on the time frame over which we view the interaction even though each run is essentially a continuous simulation because of the equal time steps used. [contsim.zip, 2k]